A Deep Reinforcement Learning Journey Home.

On a warm afternoon of October 23, 1975, one of the last days of Indian summer that year, Yozhik (aka Ejik, The Little Hedgehog) set out to visit his friend Medvezhonok (The Bear Cub). He was joining him, as he did every evening, for a night of stargazing. Only he never made a return journey home. Until now. But today the nightmares lurking in the mist the other night have become reality. Will Ejik survive?

The inspiration behind this project came from the article Deep Reinforcement Learning Doesn’t Work Yet. While whatever little experience I have with DRL (Deep Reinforcement Learning) supports the article’s conclusions it also charts a clear path for experimenting with DRL algorithms.

One advantage DRL has over vision or NLU is that its algorithms create their own labelled data, which, if you are doing research or playing in the sandbox (like me) usually comes from environments created by organizations and communities like Gym from OpenAI or ML-Agents from Unity.

While these are excellent, they don’t allow for an end-to-end exploration: the task, observations, actions, and the reward function are already given, while according to the author of the above article this is where quite a lot of fun (and frustration) of DRL happens.

And so I set out to create an environment of my own and picked Unity ML-Agents for the task. The setup is such that you create a game in Unity and then you can outfit your game characters with a “brain” (ML-Agents terminology), through which you can have them act autonomously. Unity has created several environments which show how these brains can be trained using DRL to perform various tasks. Also check out this course from Udacity to get started on DRL.

The Game

After acquiring some remedial game development skills by mostly following this course, I have created the simple Ejik Goes Home top-down shooter where the goal is simple: just stay alive for as long as possible. In reality Ejik is not going anywhere, all he can do is defend himself against 3 categories of enemies.

Even though the game can be played by a human, it was developed with Ejik in mind: he would acquire enough intelligence through DRL to play it himself.

The game is available HERE

The source is HERE

Adding Intelligence to the Main Character

Our character initially has no idea what is going on and has no access to the internal state of the game. By taking action in the environment and collecting rewards or incurring costs he is eventually able to achieve the goal the environment has set for him.

Environment and Observations

Unity environment for Ejik is simply the main and only level of the game. It can be taken over by the ML-Agent Python API with the help of which Ejik’s brain is outfitted with a trained deep neural net implemented in PyTorch.

Ejik’s view of the environment is obtained from a camera that is attached to the player (its position is always (0, 0) relative to the player himself) and gives a 300×200 pixels resolution view of the surroundings. We extract the grey scale image to use as an observation. The camera is positioned in such a way so it does not see the background.

EjikBrain properties are also set at design time. It also defines the action space explained below:

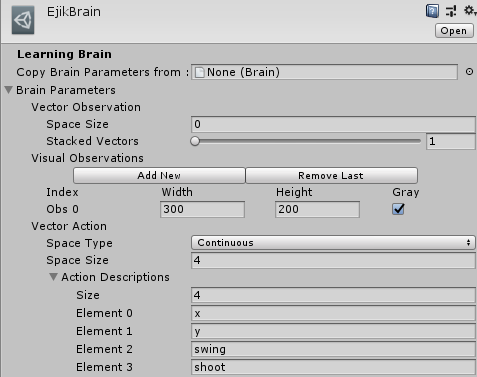
It is important not to forget to check the Control box when adding the brain to the Academy (object that oversees autonomous actions in the environment)

This will make sure the brain can be driven by an external process.

This notebook is handy for exploring the environment from Ejik’s point of view.

This is an example of a a single frame that the Ejik-attached camera sees. The camera itself is rendering to RenderTexture (a very convenient feature of ML-Agents). This setup implies that the user is responsible for the actual rendering of the image into its RenderTexture every time a new observation is required.

Observations are sent to the external brain on FixedUpdate, so this is a good place to call renderCamera.Render() where renderCamera is the camera attached.

Details on defining observations are covered in this Unity ML-Agents doc.

The motivation behind using visual rather than vector observations was:

• Ease of implementation: just render to a texture and done
• Easy to debug by simply visualizing
• Felt more interesting: the brain is going to be seeing what the character is seeing (kinda) and so whatever it learns should be all the more impressive.

Actions

We need to enable 3 types of actions:

• movement
• swinging the weapon
• shooting

So, how do we define the action space? Should it be continuous, discrete, or hybrid? While the shooting action is clearly discrete (shoot/don’t shoot), swinging is continuous rather than discrete: the angle can be anything in but we can discretize it. Movement can be either discrete or continuous depending on what we want to do: we can represent it as a direction in degrees in or a vector (x, y) that would yield the same direction in , and then it would be continuous, or we can mimic game controls and represent it as a vector of “Up”, “Down”, “Left”, “Right” discrete directions.

Eventually I decided to represent movement as a continuous action in , mainly because it’s easy to represent swinging the weapon as continuous, now shooting had to be made continuous or a hybrid space could be implemented. This paper looked promising in its treatment of hybrid action spaces, however, for the sake of simplicity in this first experiment, I made the shooting action continuous by simply mapping it over : positive value means “shoot” non-positive – “don’t shoot”.

The Game Arithmancy. Reward Function.

The player starts with 0.5 health points and faces 3 kinds of enemies: Raven, Moth, and Horse. Raven and Moth attack at set intervals and the attack lasts for some time, causing damage of 0.1 (-0.1 reward). These values (interval, duration) in sec are (5, 1) for Raven and (2, 2) for Moth. Horse does not attack, it spawns Moth. Once player health falls below 0, the player dies. The death blow cost is 0.5 instead of 0.1.

Ejik’s dandelion can shoot projectiles (with a 0.1 sec interval) and its blossom is deadly. The weapon inflicts a 0.1 damage on the enemies. Killing an enemy adds to Ejik’s (player’s) health (the player is rewarded the same number of points): 0.02 for Moth and Raven, 0.05 for Horse. Enemies possess health points as well: 0 for Moth and 0.1 for Raven. Death occurs for everyone in the game when health < 0.

Thus we get our reward function.

Ejik moves with the speed of 5, enemies with max speed of 3 for Raven and 2 for Moth. Horse doesn’t move. The A* Pathfinding component is in charge of guiding the enemies towards player.

An episode consists of 3000 steps, for which the current goal is to survive. A more complex goal would be to get some positive reward, but that’s for later.

Rewards correlate directly with health, but while initial health = 0.5, initial reward = 0, so it is possible to survive an episode and get a negative reward. Dying before the episode ends will always cause the reward to be < -0.9 (lose all health and get a -0.5 bonus on top of it). Minimal possible reward is -1.0.

The number of enemies is parameterized, enemies are generated spontaneously once there are too few of them in the game, generation stops once there is enough. This only applies to Raven and Horse, since Moth is spawned by Horse at fixed intervals while Horse exists. Enemies appear at random points in the scene outside a certain radius away from the player. Training was done with 1 <= Raven <=3 and maximum 1 Horse, however, during evaluation number of Ravens was increased to [3, 6].

Model Input

Each of the 3000 steps in one episode occurs on Unity physics update (FixedUpdate), which happens every 0.02 seconds. The input to the model consists of 6 game frames each grabbed at 3 frame intervals. Thus during 3000 steps there are decisions, i.e. action vectors that the model outputs, or fewer if Ejik dies prematurely.

Once the episode ends, the environment resets, i.e. Ejik is returned to the (0,0) coordinate of the level and his health is set to 0.5.

Random Play

Let’s check out what happens in the environment if we are making random decisions.

If we collect game stats over 1000 random episodes we will get:

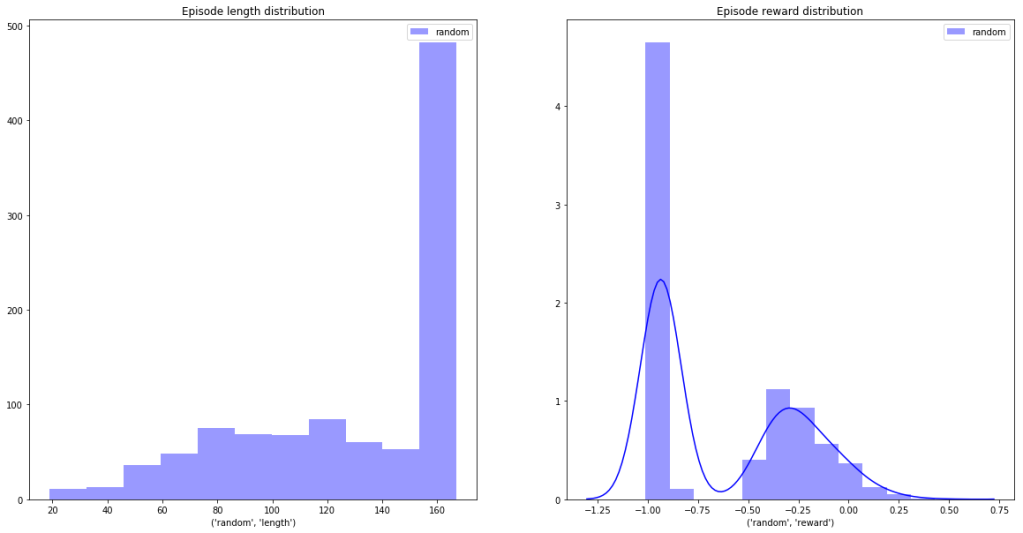
Histogram of survival time (maximum 167) on the left, distribution of rewards – on the right.

Thus played at random we mostly die: the -1.0 “death bar” is prominently featured on the reward distribution and certain survival happens less than half the time (number of steps in an episode =167).

Unfortunately it turns out that beating the random game is easy. While our random play was:

actions = np.random.randn(4)

We need but minimal determinism: shoot for sure at every step:

actions = np.r_[np.random.randn(3), [0.5]]

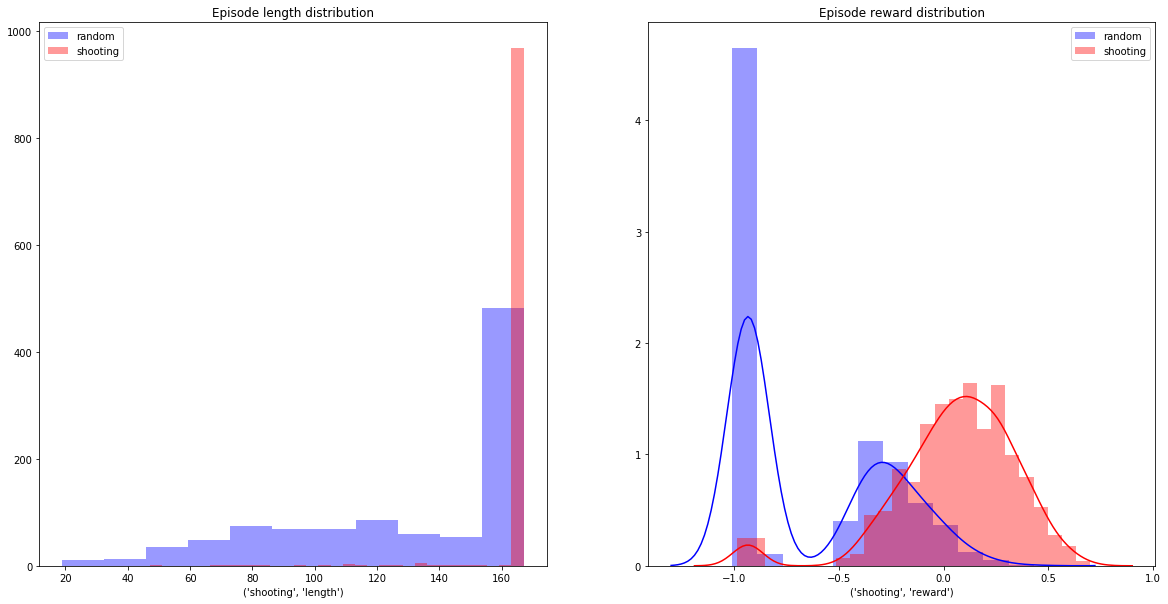
Immediately we start surviving rather than dying with virtual certainty.

Still it would be interesting to see if at the very least a DRL algorithm can learn this simple strategy. After all, mapped to the spectrum between Tic-tac-toe and Go, we are closer to the former, so “simple” is not unexpected.

Model and Algorithm

The PPO algorithm seems an obvious choice due to:

• ease of implementation
• promise of fast convergence

This is a policy-based Actor Critic algorithm where we assess the advantage (critic) of an old policy and guide the evolving policy (actor) towards maximizing this advantage. I also like it because it is on-policy, so we can go through a sequence of steps and discard our data right away, no need for a replay buffer with its memory demands.

The code for this implementation is on my GitHub.

After some experimentation, the model I picked was this (details are in drl\PPO\model.py):

Both Actor and Critic share a CNN feature extractor:

    def hidden_layers(self):
        return [
            nn.Conv2d(self.state_dim[0], 16, 4, stride=4),
            nn.LeakyReLU(),
            nn.Conv2d(16, 32, 3, stride=2),
            nn.LeakyReLU(),
            nn.Conv2d(32, 64, 3, stride=2),
        ]

here self.state_dim[0] is the number of stacked frames (6 in our case), the CNN wants its input tensors in the NCHW format (N-batch size, C-number of channels, 6 in our case, H – height, W – width – 200 and 300 respectively)

The rest of the layers for Critic and Actor are:

        self.fc_hidden = self.hidden_layers()
        fc_critic = self.fc_hidden \
            + [Flatten(), 
                nn.Linear(conv_size, conv_size // 2),
                nn.LeakyReLU(),
                nn.Linear(conv_size // 2, 1)]

        fc_actor = self.fc_hidden \
            + [Flatten(), 
                nn.Linear(conv_size, conv_size // 2),
                nn.Tanh(),
                nn.Linear(conv_size // 2, self.action_dim), 
                nn.Tanh()]

        self.actor = nn.Sequential(*fc_actor)
        self.critic = nn.Sequential(*fc_critic)
        self.log_std = nn.Parameter(torch.zeros(1, act_size))

Since the action output is a vector of means of a multivariate Gaussian, we also need a vector to represent the variances, so we can fully represent a distribution from which final actions will be computed.

I used Adam optimizer with a slowly decaying learning rate which started at . The details are in drl\PPO\driver.py

Training and Evaluation

The model as described trains for ~10-12 hours while the game runs at 10 times the regular speed. So 600 games/hr are played and the brain catches on after about 6000 games and doesn’t improve after that. The entire process can be observed in Tensorboard. Tensorboard consumable events are output to the runs subdirectory.

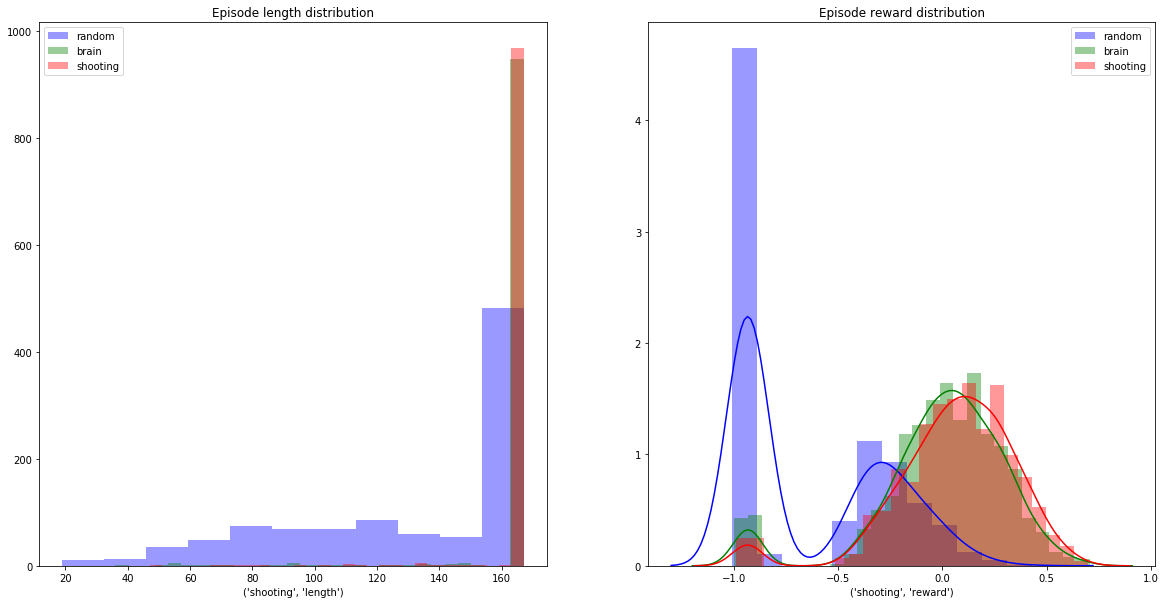
We evaluate our model, as before, by playing 1000 games. Here is the comparison of the resulting brain activity with random and minimally-deterministic strategies described above (all charts are generated by the Ejik Analysis notebook):

The resulting weights can be downloaded here. drl\PPO\eval.py can be used to run the environment after building the MainScene in Unity.

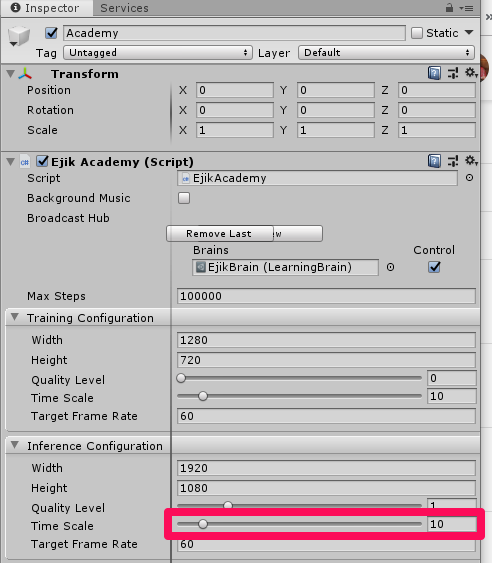
In the Academy object, EjikAcademy component, Inference Configuration / Time Scale needs to be changed to 1 before building for real-time replay.

Conclusions

Clearly, we have achieved our survival goals. The brain powered by our AI survives almost as well as the minimally-deterministic strategy. It is disappointing, though, that we didn’t do better, considering the simplicity of our non-AI strategy.

For the future, it would be interesting to investigate a more “strict” reward function: assign cost to shooting, disable the weapon ability to cause touch damage, make enemies more threatening by decreasing attack intervals, etc.

It would also be interesting to investigate the hybrid action model, where shooting decision remains discrete.

Finally, making the game purely DRL based where all participants truly “know not what they do” initially but as training progresses gradually fall into their roles.

Or perhaps raising the stakes all around is the way to go. Perhaps a brand-new more complex game is in order!